Por Gustavo Mirapalheta
Para responder a esta pergunta vamos para um experimento no Excel. O que acontecerá com o histograma das respostas se forem feitas 100.000 pesquisas não com um respondente apenas, mas com a média de trinta respondentes? Veja bem, agora teremos 100.000 pesquisas de uma pergunta, porém cada pesquisa terá como resultado a média das respostas de 30 pessoas. A primeira vista, nada de especial deverá ocorrer, afinal estamos somando 30 resultados entre 0 e 1 e dividindo por 30. Ou será que a matemática esta prestes a nos pregar uma peça? Para tirar a limpo esta dúvida, vamos fazer 100.000 células e em cada uma calcular a média de 30 funções aleatório(). Feito isso vamos refazer o histograma das 100.000 pesquisas. Observe o resultado na figura abaixo:
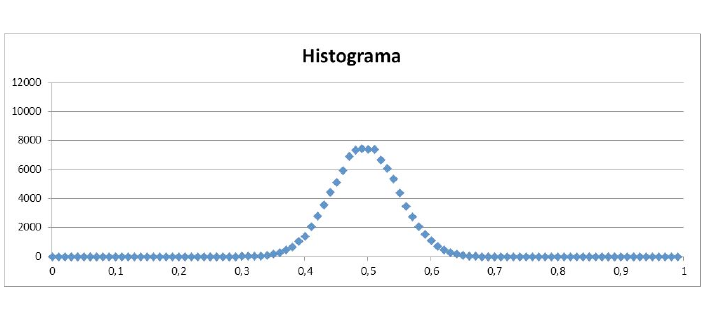Figura 3 – Histograma, 100.000 pesquisas, média de 30 respondentes cada
Impossível não passar a mão na cabeça e se perguntar o que é que esta ocorrendo aqui… O resultado é ainda mais fantasmagórico (☺), pois o pico do histograma (o valor mais provável de ocorrer) aponta para qual valor? 0,5, a média da população.
A natureza funciona de um jeito tal, que se você aumentar o número de elementos em uma pesquisa, a média da pesquisa (isto é de uma amostra) terá uma probabilidade cada vez maior de ficar bem próxima da média da população. Isto é até algo de se esperar, mas que para isto bastem 30 elementos em uma população de dezenas de milhões é o que é surpreendente. Em outras palavras, a Matemática garante que para você conhecer a média das respostas de uma população de dezenas de milhões de respondentes basta você conhecer a média das respostas de uns poucos respondentes escolhidos ao acaso (isto é muito importante, mas iremos discutir este assunto, a aleatoriedade das escolhas que irão compor a pesquisa em outra oportunidade)
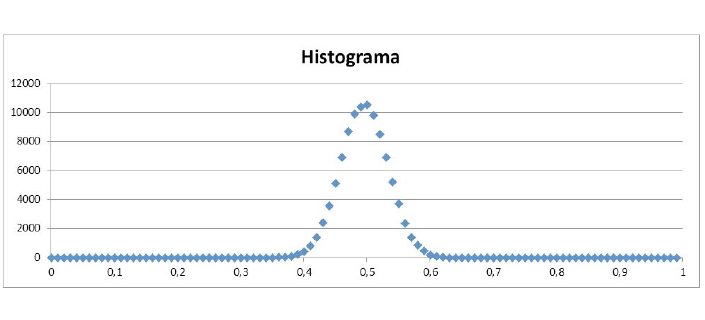
Se for aumentado o número de respondentes em cada pesquisa, o que ocorrerá? No histograma anterior, o pico ocorre com máximo de quase 8.000 respostas próximas de 0,5. Na figura abaixo é mostrado o histograma da média de 60 respondentes por pesquisa (em termos matemáticos, 60 elementos por amostra).
Como pode ser visto mais e mais a média das respostas se concentra próximo da média da população. Antes o pico ocorria com menos de 8.000 casos. Agora, o pico ocorre também em 0,5 com mais de 10.000 casos, ou seja, quanto maior for o número de respondentes de uma pesquisa, maior a probabilidade da média da pesquisa ser muito parecida com a média da população.
A curva que o histograma das médias das pesquisas forma chama-se curva normal ou gaussiana. Não importa o formato do histograma da população original (neste exemplo ele era mais ou menos um retângulo, mas poderia ser uma curva com dois picos ou outro formato qualquer), a distribuição da média das respostas sempre vai tender para uma normal, à medida que o número de respondentes por pesquisa (isto é por amostra) crescer.
Este é o resultado que mostra porque a Estatística funciona. Pegue uma pequena quantidade de pessoas, escolhidas ao acaso, pergunte o que cada uma delas pensa a respeito de um assunto e forme a média das respostas deste grupo. Pode ter certeza, que se as pessoas forem escolhidas ao acaso, a média deste grupo será muito parecida com a média da população toda, e sua distribuição seguirá uma curva denominada normal ou gaussiana. Eu aqui não preciso pedir para que acreditem em mim, basta olhar para os gráficos acima, ou repetir os experimentos no Excel no seu próprio computador. Finalizando, este resultado é chamado em Estatística de Teorema do Limite Central.
