Por Gustavo Mirapalheta
Professor ESPM
Seja em épocas de eleição, seja na simples interpretação de notícias no dia-a-dia, as pessoas se defrontam rotineiramente com conceitos de probabilidade e estatística. Todos os dias falamos das chances do nosso time ser campeão da Libertadores, da probabilidade de ganhar na Mega-Sena ou da margem de erro das próprias pesquisas eleitorais.
O tópico pesquisa eleitoral é muito interessante, porque através dele a Estatística foi sendo comprovada, ano sim, ano também, através de previsões feitas a partir de umas poucas centenas de pessoas, as quais anteveem resultados em eleitorados compostos de dezenas de milhões de eleitores. Neste caso o público se acostumou com estes conceitos simplesmente porque eles funcionaram tantas vezes que até mesmo os candidatos que estão prestes a perder uma eleição pararam de duvidar das previsões.
Para os professores fica a tarefa de demonstrar, em uma hora e quarenta minutos, porque a Estatística funciona. A tarefa é um pouco mais complicada, porque o “respeitável público” de nossas aulas é uma plateia exigente, com pouca paciência para aguentar raciocínios abstratos (do tipo: imagine uma vaca cilíndrica…) ou explicações muito longas e complicadas (afinal a tentação esta logo ali, no browser, logo depois do enter, bastando para isso teclar http://www.google.com ou http://www.youtube.com). O que a garotada prefere é “ver na prática” ou então “entender onde se aplicará o conceito x na vida real”.
Até bem pouco tempo atrás o máximo que um desafortunado professor de Estatística que estivesse diante de tal plateia poderia fazer seria dizer “acreditem em mim, pois funciona” ou então, se ele fosse corajoso o suficiente e a plateia estivesse disposta a viver fortes emoções, ele poderia entrar por uma daquelas demonstrações matemáticas que fariam até mesmo um crente duvidar de sua fé (nos números, neste caso).
Modernamente, com o advento dos computadores e em especial das planilhas eletrônicas, algumas opções estão disponíveis a este intrépido professor de Estatística. Se as demonstrações matemáticas continuam abstratas, pode-se pelo menos gerar uma pesquisa simulada com 1.000, 10.000, 100.000 ou quem sabe 1.000.000 de respondentes e ver a Estatística funcionando “na prática”. É isto que se pretende mostrar aqui.
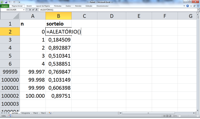
Planilhas eletrônicas como o Excel, incluem um recurso bem pouco conhecido, chamado sorteio ao acaso, ou aleatório. É uma função que, toda vez que é executada pela planilha, tira um número entre 0 e 1, ao acaso, de uma urna virtual, a qual contém dezenas de milhões de números, todos com igual probabilidade de sair. A função se chama aleatório().
Sendo assim, vamos sortear 100.000 números ao acaso e depois fazer um gráfico contando, entre zero e um, de 0,01 em 0,01, quantos números saíram em cada intervalo. Em outras palavras, vamos fazer um histograma dos 100.000 valores.
Agora para interpretar “na prática” o que estamos fazendo, é necessário pensar que temos aqui 100.000 pesquisas de marketing de pergunta única. Cada pesquisa teve apenas um respondente, e a resposta que ele deu foi um número entre zero e um.
Figura 1 – 100.000 “pesquisas” de 1 respondente cada
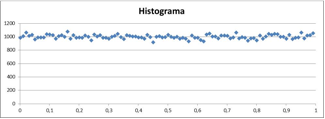
Seguindo em nosso raciocínio, temos aqui uma população potencial de dezenas de milhões de números, todos entre 0 e 1, e desta população tiramos 100.000 números, isto é, fizemos 100.000 pesquisas de marketing. Uma conta bem simples, mostra que teremos aproximadamente em cada intervalo de 0,01 dos possíveis resultados nas pesquisas, 100.000 x 0,01 = 1.000 elementos, o que pode ser visto no gráfico abaixo.
Figura 2 – Histograma, 100.000 pesquisas, 1 respondente
Agora vem uma parte importante. A média das respostas é 0,5, ou seja, a opinião média dos respondentes é 0,5, pois eles todos estão entre 0 e 1 e qualquer resposta neste intervalo tem igual probabilidade de sair. Isto pode ser visto tanto no gráfico acima quanto por um cálculo fazendo (0 + 1)/2 = 0,5.
No entanto, não é possível prever esta média olhando apenas uma resposta, pois por definição ela pode dar qualquer resultado entre 0 e 1. Sem saber de antemão que os resultados ficam sempre entre 0 e 1, e que todos os resultados tem igual probabilidade de sair é impossível dizer algo sobre a média do conjunto olhando apenas um elemento. Em outras palavras, saber que o respondente número 1.134 respondeu 0,798 não diz nada de muito útil a respeito do conjunto dos respondentes. 0,798 talvez seja um daqueles resultados únicos, tipo aquele time do interior que um dia ganhou uma final do time da capital e depois foi rebaixado para a Segunda Divisão no ano seguinte.
Suponha agora que é você tentando descobrir esta média, sem ter acesso aos 100.000 respondentes, nem qualquer informação específica a respeito da população, apenas a 30 (isso mesmo, trinta) respondentes. Será que a média das respostas destas trinta pessoas não poderia dizer algo de útil sobre a média das dezenas de milhões de números da população?