Por Cléber da Costa Figueiredo
Você já parou pra pensar porque se estuda tanto a normalidade como um resultado da estatística teórica? Sim, a normalidade do modo como é estudada nas universidades é um resultado estatístico teórico. A simetria, a quantidade de vezes que um fenômeno se distancia da média, ora acima ora abaixo dela é um resultado teórico.
Contudo, quando se aborda um processo experimental, ou de produção, com o intuito de se trazer para a perspectiva de uma empresa, nestes casos, percebe-se quão importante foi entender o conceito estatístico de normalidade.
O tempo que se leva para realizar uma determinada tarefa contábil, a quantidade de sal que se coloca em um alimento de uma cozinha industrial (inclusive a informação nutricional no rótulo de um alimento), o envazamento de um xampu numa linha de produção são exemplos de fenômenos que são regidos pela normalidade. Em que isso afeta o empresário?
Que a probabilidade de se produzir ou de processar itens fora das especifícações é um valor fixo. O que se pode controlar, no entanto, são parâmetros como a média ou a variabilidade (medida pelo desvio padrão). Daí o termo seis sigmas, que faz analogia a três desvios acima ou abaixo da média. Que, teoricamente, indica que os fenômenos estarão nesse intervalo em 99,73% das vezes.
Nesse sentido, é que se desenvolveu o conceito de qualidade total, uma vez que a redução da variabilidade do processo está diretamente relacionada à qualidade.
Qualidade é produzir tudo do mesmo modo, com a mesma quantidade, com o mesmo tamanho. Quando se refere a um processo, é não alterar as regras no meio do caminho. É entregar o serviço sempre da mesma maneira. É manter um canal de atendimento com o cliente, é esclarecer as dúvidas e resolver conflitos.
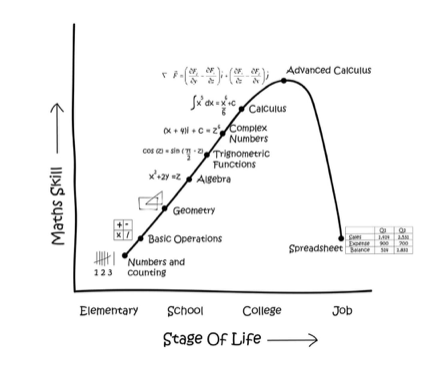
A motivação para a escrita deste texto foi a figura abaixo que está circulando nas redes sociais:
A lógica matemática por trás disso tudo é muito evoluída. Para entender que, a chance de um fenômeno ocorrer três desvios acima ou abaixo da média é de 99,73%, é preciso ter aprendido que a probabilidade é uma medida. Assim como o litro, o metro, a onça, a polegada. Que é uma medida de uma área sob uma curva em forma de “sino”. Que não há uma integral indefinida elementar para a função gaussiana. Oi?
Que as aproximações algébricas para o cálculo dessa área, serão calculadas, numericamente, via algum software que utiliza alguma solução para a soma dos retângulos superiores e inferiores de Riemann. Aqui, força-se a amizade.
Deixa para lá, no fundo tanto faz, porque é uma mera probabilidade. No dia a dia, o Excel resolverá isso. Ou não? Foi assim com o litro, com o metro, com a onça, com a polegada. Será assim com a probabilidade.